Se le cose non sono andate bene, quando una persona esce da un casinò non potrà che chiedersi “Perché ho perso?” La maggior parte delle persone che frequentano i casinò finiscono per perdere e questo perché la maggior parte dei giochi da casinò ha per natura un'aspettativa negativa. Ciò significa che, per ogni puntata effettuata, la macchina o il gioco da tavolo restituisce una quantità di denaro inferiore a quella scommessa.
Se un milione di giocatori scommettono un dollaro e un giocatore vince 500.000 dollari, il casinò guadagna 500.000 dollari e ogni scommessa ha una perdita media di 50 centesimi. Nelle slot machine il rimborso pubblicizzato è spesso intorno al 97-99%. Questo è calcolato per l’intera vita della macchina, durante la quale può arrivare a raccogliere centinaia di milioni di dollari. I giochi da tavolo sono leggermente diversi, perché alcuni includono una componente di abilità e il vantaggio che il casinò acquisisce varia da giocatore a giocatore. Detto questo, il principio generale rimane lo stesso.
Questo articolo offre un'analisi approfondita della matematica dei giochi da casinò. Le informazioni contenute sono valide sia per il blackjack ai tavoli sia per il gioco online. Tuttavia, i software utilizzati dai casinò online includono tutte le carte in ogni nuovo round di gioco. Il blackjack è un gioco di probabilità dinamiche e percentuali variabili: pur se le percentuali cambiano costantemente, la percentuale cumulativa del vantaggio complessivo rimane la stessa.
Questa si ottiene facendo la somma di tutti i margini di tutte le possibilità. Se il totale di una mano ha un vantaggio positivo del 5% e quello di un'altra uno negativo del -6%, il vantaggio totale per entrambe le mani è -1%. Capito questo schema sarà possibile applicarlo a qualsiasi altro gioco da casinò con vantaggio statico sul giocatore.
LE STATISTICHE
Le comprensione delle statistiche dei giochi da casinò è essenziale e ciò vale sia per il giocatore sia per i casinò. Le nozioni presentate in questo articolo sono necessarie per determinare se i risultati, buoni o cattivi che siano, siano possibili oppure no.
La maggior parte dei giochi d'azzardo riflette il concetto matematico delle cosiddette prove indipendenti. Esso afferma che gli eventi passati non hanno alcuna rilevanza sugli quelli futuri. Ciò è facilmente comprensibile alla roulette e ai dadi; oppure quando una moneta viene lanciata: la probabilità sia che esca testa sia che esca croce è sempre del 50%.
Se per dieci volte di fila esce testa, al lancio successivo la probabilità che esca testa è di nuovo del 50%. A blackjack invece ciò che è accaduto in precedenza influenza direttamente ciò che accadrà ora: si potrebbe dire che il blackjack abbia una memoria e che la legge dei processi indipendenti in questo caso non sia valida.
IN CHE MODO SI DIFFERENZIA IL BLACKJACK?
A blackjack ogni carta ha un valore specifico che si aggiunge o si sottrae al vantaggio iniziale del casinò sui giocatori. Esso è determinato dalle regole applicate. Se esce un numero sufficiente di carte di un certo tipo, i giocatori possono ritrovarsi ad avere un vantaggio. A blackjack il vantaggio del casinò aumenta quando viene distribuito un asso o una carta di valore 10, mentre diminuisce quando vengono distribuite carte di basso valore, ovvero dal 2 al 7. Una volta uscito un numero sufficiente di tali carte, i giocatori si trovano in condizione di vantaggio rispetto al casinò.
Il vantaggio percentuale che il casinò ha sul giocatore e viceversa non è statico a blackjack. Esistono molti approcci che consentono di tracciare tali cambiamenti: il più semplice e meno soggetto a errore è il conteggio Hi/Lo. Tale sistema assegna alle carte valori pari a 1, -1 e 0 . A tutte le carte dal 2 al 6 viene assegnato il valore 1, dal 7 al 9 il valore 0, a tutte le decine, figure e assi il valore -1. Man mano che le carte vengono distribuite, il giocatore effettua la somma, il cui risultato è definito conteggio corrente.
In un conteggio positivo, il valore viene normalizzato in una media di quante più carte alte rispetto alle carte basse (o carte basse rispetto alle carte alte) vi sono per mazzo. A tale scopo, il giocatore stima il numero di mazzi rimanenti e il conteggio corrente viene diviso per il numero di mazzi rimanenti: tale valore viene definito conteggio reale. Se un giocatore ha osservato tre mazzi di un distributore da sei mazzi e il conteggio corrente è 15, significa che in quei tre primi mazzi sono state giocate quindici carte basse dal 2 al 6 in più rispetto alle carte alte come dieci, figure. Il conteggio corrente di valore 15 viene quindi diviso per i mazzi rimanenti, ovvero tre: il risultato è un conteggio reale di cinque.
Il giocatore sottrae un valore, di solito 1, che corrisponde al vantaggio del casinò a inizio mazzo: esso dipende da diversi fattori come le regole applicate e il numero di mazzi utilizzato. Il risultato di tale sottrazione è il numero di unità che il giocatore scommetterà nella mano seguente. Per ogni incremento intero di unità (positivo o negativo) nel conteggio reale, il vantaggio di un giocatore aumenta o diminuisce di circa lo 0,5%.
Quando si ha una preponderanza di carte alte, il conteggio reale è alto e il giocatore ha un vantaggio rispetto al casinò. Ciò si verifica per tre motivi. In primo luogo i blackjack vengono distribuiti più frequentemente, e la vincita su un blackjack è asimmetrica (ovvero il blackjack viene pagato 3 a 2 a un giocatore, mentre in caso di blackjack del banco lo stesso giocatore perde solo la puntata iniziale).
In secondo luogo alcune delle opzioni possibili diventano più preziose, come dividere una coppia e raddoppiare. Quando un giocatore raddoppia o divide spera di ottenere una carta alta, oppure lo fa quando il banco è debole e una carta alta potrebbe farlo sballare. Queste giocate hanno un rendimento più elevato quando il mazzo di carte rimanente è ricco di carte alte.
Infine un giocatore può variare la propria strategia in base alla composizione delle carte rimanenti. Con una preponderanza di carte alte può rimanere su mani hard dal 12 al 16, raddoppiare più spesso con mani forti dal 9 all'11 o rimanere quando il banco è debole e rischia di sballare. Le regole impediscono invece al dealer di variare la propria strategia: la combinazione di tali fattori crea condizioni nelle quali il vantaggio del casinò viene ribaltato e favore di un giocatore esperto capace di sfruttare la situazione.
CALCOLARE LA PROPRIA VINCITA
Per determinare l'importo che ci si aspetta di vincere in un determinato momento, sia per il casinò sia per il giocatore, sono necessarie tre informazioni:
1. La dimensione della scommessa;
2. Il numero di mani o giri;
3. Il vantaggio percentuale.
SOTTO FORMA DI EQUAZIONE, TALE DICHIARAZIONE SI ESPRIME NEL MODO SEGUENTE:
Vincita prevista in $ = scommessa in $ * vantaggio% * # mani giocate
EQUAZIONE 1
Facciamo l'esempio di una moneta: ha due facce e le probabilità che esca testa o che esca croce sono entrambe del 50%. Scommettendo 1 dollaro per lancio, queste sono le prospettive di vincita per 100 lanci:
50$ = 1$ (scommessa) * 0,5% (vantaggio%) * 100 (# mani giocate)
EQUAZIONE 2
Alla fine non abbiamo né vinto né perso. Scommettendo un totale di 100$, abbiamo vinto 50$ in 50 scommesse e mantenuto 1$ di quelli originali in 50 di quelle 100 scommesse. Allo stesso tempo abbiamo perso 1$ in 50 di quelle scommesse. La somma è pari a zero: nessun vincitore, nessun vinto.
È ESATTAMENTE COSÌ?
Quando una moneta viene lanciata 100 volte, raramente uscirà esattamente 50 volte testa e 50 volte croce. Dobbiamo quindi introdurre il concetto di varianza per numero di eventi: essa è una misura della dispersione statistica. In parole povere, la varianza descrive la deviazione di un risultato dal valore atteso durante una prova o un esperimento.
Rimanendo all'esempio del lancio della moneta, la varianza aiuta a rispondere alla seguente domanda: sarebbe sorprendente se uscisse testa 45 volte su 10? E lo sarebbe se uscisse solamente cinque volte su 100? Le risposte sono rispettivamente no e sì. Dovesse uscire testa solo cinque volte, probabilmente si starebbe usando una moneta truccata. Si tratta di un concetto cruciale per poter valutare i risultati al casinò: un'analisi statistica adeguata è assolutamente necessaria per determinare se tali risultati, buoni o cattivi che siano, siano frutto della fortuna o dell'abilità. Ciò determina chiaramente se un giocatore o un casinò venga ingannato o meno.
La varianza è di solito definita in termini di deviazioni standard e come tale verrà trattata in questo articolo. La deviazione standard è uguale alla radice quadrata della varianza; per una serie di prove è rappresentata dalla lettera greca σ (sigma) ed è uguale alla deviazione standard di ciascun evento moltiplicata per la radice quadrata del numero di eventi. La formula matematica è la seguente:
σ (totale) = σ (evento) * √ (Numero di eventi)
EQUAZIONE 3
L'immagine seguente mostra la probabilità che i risultati rientrino in una, due e tre deviazioni standard del risultato atteso. Nella rappresentazione grafica il valore atteso è indicato dalla lettera greca µ e la deviazione standard è rappresentata dalla lettera greca σ.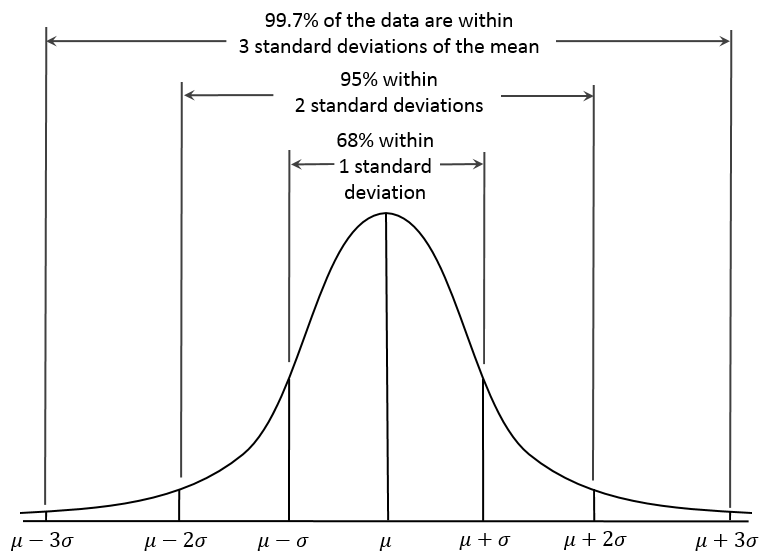
Secondo la curva di distribuzione gaussiana, la probabilità che il risultato sia compreso all'interno di una deviazione standard, positiva o negativa, del valore atteso è di oltre il 68%; inoltre la probabilità che esso sia compreso entro due deviazioni standard, positive o negative, del valore atteso è di poco superiore al 95%; infine la probabilità che il risultato cada entro tre deviazioni standard, positive o negative, del valore atteso è di circa il 99,9%.
Applicando questa teoria ai 100 lanci di una moneta, la deviazione standard per 100 prove è equivalente a 10, ovvero radice quadrata di 100, moltiplicato per la deviazione standard per una singola prova, ovvero 0,5. Ciò risulta in una deviazione standard pari a 5. Nel caso del lancio della moneta, ci aspettiamo che in 50 lanci su 100 esca testa e negli altri 50 su 100 esca croce. Includendo il concetto di deviazione standard di +/-5, possiamo dire che esiste un 68% di probabilità che per ogni 100 lanci esca testa tra le 45 e le 55 volte.
Allo stesso modo, esiste un 95% di probabilità che per ogni 100 lanci esca testa tra le 40 e le 60 volte (2*σ) e un 99,9% di probabilità che esca tra le 35 e le 65 volte (3*σ).
Applicando le equazioni del risultato atteso e della deviazione standard ai 100$ scommessi a un gioco da casinò con un vantaggio della casa dell'1%, risultano i seguenti valori: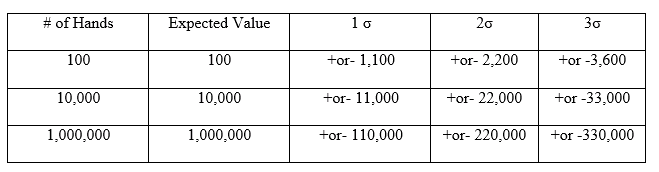
Lo stesso si può raffigurare graficamente come segue: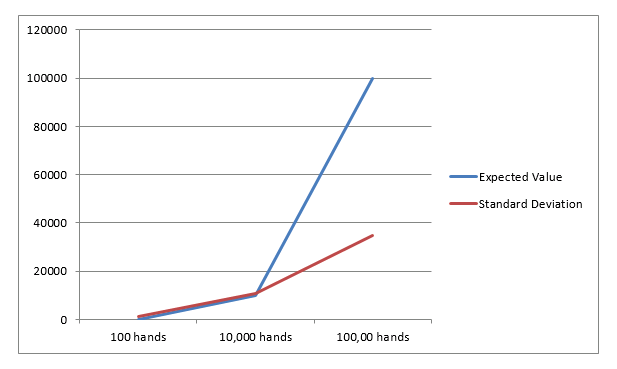
All'aumentare del numero di eventi, la deviazione standard diventa sempre più bassa rispetto al risultato atteso. A un certo punto, il risultato atteso e le deviazioni standard s'intersecano: a partire da lì la probabilità che la deviazione standard sia inferiore al risultato previsto è dell'84%. Ciò significa che esiste una probabilità dell'84% che da quel punto in poi si realizzi un profitto e che il proprio bankroll non venga delapidato. Il grafico seguente mostra il punto d'intersezione per un gioco da casinò con un vantaggio dell'1%: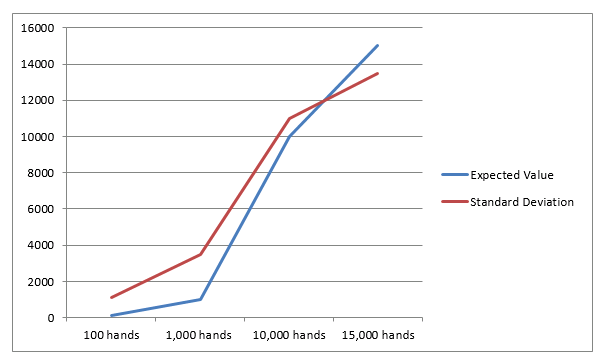
PER SEMPLICARE, IL VALORE DELLA DEVIAZIONE STANDARD È ESPRESSO IN TERMINI ASSOLUTI
Il punto d'intersezione tra il risultato atteso e la deviazione standard è appena sotto le 12.000 mani. A partire da 12.000 mani la probabilità che il rsultato atteso superi la deviazione standard negativa è dell'84%, il che significa che nell'84% dei casi il giocatore non dilapiderà il proprio bankroll. Se il vantaggio complessivo aumenta, il punto di equivalenza, ovvero il numero di mani in corrispondenza del quale il risultato atteso è uguale alla deviazione standard, viene raggiunto con un numero di mani inferiore. Calcolando lo stesso grafico con un vantaggio della casa del 2%, esso mostra un punto di equivalenza sostanzialmente inferiore: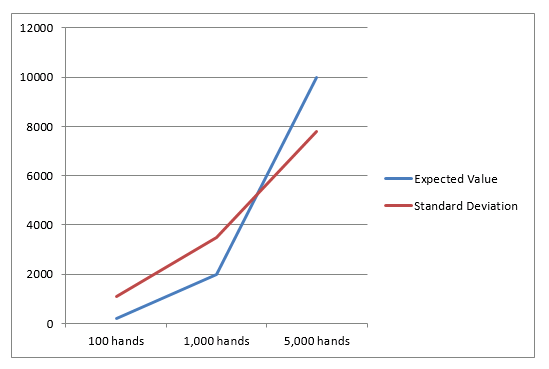
PER SEMPLICARE, IL VALORE DELLA DEVIAZIONE STANDARD È ESPRESSO IN TERMINI ASSOLUTI
In ultima analisi, i casinò sono in grado di raggiungere in modo estremamente rapido il punto di equivalenza e questo perché vi si gioca 24 ore al giorno e sette giorni alla settimana. E poiché quasi tutti i giocatori partono da una condizione di svantaggio, i casinò guadagnano sempre più soldi con una varianza sempre più bassa rispetto al loro risultato atteso. Nei prossimi articoli illustrerò alcuni metodi per attaccare i giochi da casinò e ottenere maggiori profitti.


